A ne lire que si vous aimez les détails...
- si $(u_n)$ est constante, alors, il existe une infinité de couple $(a,b) $ tels que $u_{n+1}=au_n+b$
- sinon $a$ et $b$ sont uniquement déterminés par $u_0$, $u_1$ et $u_2$ ; et donc $(u_n)$ ne dépend que de $u_0 $, $u_1$ et $u_2$.
Cas où $(u_n)$ est constante
Dans cette partie $(u_n)$ est constante.
Notons $f$ la fonction telle que $f(x)=ax+b$. Si $a\neq 1$, on note $s$ le point fixe de $f$, c'est-à-dire le point $s=\frac{b}{1-a} $.
Supposons dans un premier temps que $a\neq 1$.
Si $u_0=s$, alors $u_1=f(s)=s $ et de même $u_2=f(u_1)=f(s)=s$, etc. (faire une récurrence pour la rigueur). Donc la suite est constante : pour tout entier naturel $n$, $u_n=s$.
Remarquons au passage que $u_0=0 $ si et seulement si $s=\frac{b}{1-a}=0\Leftrightarrow b=0 $.
Réciproquement, si la suite est constante, $u_0=f(u_0) $ donc $u_0=s$ car c'est l'unique point fixe de $f$ quand $a\neq 1$.
En général, comme la suite est constante, on peut écrire la relation de récurrene de la suite de plusieurs façons :
- $u_{n+1}=au_n+b $
- $u_{n+1}=u_n $
Peut-on écrire cette suite constante avec une autre relation $u_{n+1}=a'u_n+b' $ ? Comme $u_1=u_0=s$, $s$ est la seule solution de l'équation $a'x+b'=x $, donc $s=\frac{b'}{1-a'} $.
Donc $\frac{b}{1-a}=\frac{b'}{1-a'} $.
Soit $b'$ un réel non-nul, alors $1-a'=\frac b {b'(1-a)} $, donc $a'=\frac b {b'(a-1)}+1 $.
Si $b'=0$, alors d'après la remarque précédente, on peut écrire pour tout réel $a'$, $u_{n+1}=a'u_n $.
En résumé, si la suite est constante avec $u_n=s$, on peut définir la suite de plusieurs manières différentes $u_{n+1}=au_n+b $ pourvu que $s=\frac{b}{1-a} $. Dans le cas pariculier où $s=0 $,tout $a$ peut convenir tant que $b=0$.
Réciproquement si on peut écrire la suite de différentes manières, cela implique-t-il que la suite est constante ?
Nous aurons la réponse plus tard.
Maintenant si la suite est constante avec $a=1$, c'est-à-dire si pour tout $n$, $u_{n+1}=u_n $, alors on a aussi $u_{n+1}= a'u_n+b'$ dès que $u_0$ est un point fixe de $g$ où $g(x)=a'x+b'$. Or si $b'>0$, $g$ n'a aucun point fixe et si $b'=0$, $g$ n'a que des points fixe, et on retombe sur la relation $u_{n+1}=u_n $. Donc ce n'est possible que lorsque $a'\neq 1 $ et $u_0=\frac{b'}{1-a'} $.
Cas d'une suite non-constante
Dans le cas d'une suite non-constante et telle que $a\neq 0$, tous les termes de la suite sont distincts deux à deux.
De plus, si $a=1$, alors $b\neq 0$ et si $a\neq 1$, alors $u_0\neq s $.
Est-ce que $a$ et $b$ sont uniquement déterminés par les termes de la suite $(u_n) $ ?
On a $u_1=au_0+b $ et $u_2=au_1+b $.
On en déduit que
En termes matriciels,
Le déterminant de la matrice
est $u_0-u_1 $. Comme la suite $(u_n)$ n'est pas constante, il est donc non-nul et la matrice possède une inverse :
On en déduit que $a$ et $b$ sont uniquement déterminés par $u_0$, $u_1 $ et $u_2$ :
Donc
On retrouve que si $u_1=u_2$, $a=0$ et $b=\frac{u_1(-u_1+u_0)}{u_0-u_1}=u_1$ et la suite est constrante à partir du rang 1.
Donc si la suite n'est pas constante, $a$ et $b$ sont uniquement déterminés par ses éléments ($u_0$, $u_1$, et $u_2$ suffisent).
En particulier puisque $u_0$, $a$ et $b$ définissent entièrement $(u_n)$, une suite arithmético-géométrique ne dépend que de $u_0$, $u_1$ et $u_2$.


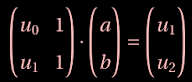
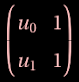



Aucun commentaire:
Enregistrer un commentaire