Spécialité Maths - Exercice 9 - Une solution

Voici la solution  un exercice niveau Terminale de la spécialité mathématique.

Des versions téléchargeables (pdf et tex) sont disponibles à la fin de l'article.  

Thèmes. Fonctions trigonométriques, équation

Niveau Terminale de la spécialité mathématique.

Exercice 9.

Combien y a-t-il de soltuions dans l'intervalle $[0;2]$ à l'équation $$\sin\left(\pi x(1-x) \right)=0,7$$

La solution 

Définissons une fonction $f$ sur $[0;2]$ par $f(x)=\sin\left( \pi x(1-x) \right)$.

$f$ est la composée $u\circ w$ de 2 fonctions $u$ et $w$ définies par

• $w(x)= \pi x(1-x)= \pi (-x^2+x)$
• $u(x)=\sin(x)$

où $w$ est définie sur $[0;2]$ et $u$ est définie sur l'intervalle image de la fonction polynomiale, dérivable (et donc aussi continue) $w$ (comme $u$ est la restriction de la fonction sinus définie et dérivable sur $\mathbb R$).

Ainsi $f$ est dérivable sur $[0;2]$, et on a $f'=w'\cdot u'\circ w$.

On a pour tout $x$ dans l'intervalle de définition de nos fonctions respectives

• $w'(x)= \pi (-2x+1)$
• $u'(x)=\cos(x)$

Ainsi pour tout $x\in[0;2]$,

$$f'(x)=w'(x)\cos(w(x))= \pi \left(-2x+1\right)\cos\left( \pi x(1-x) \right)$$

Etudions les variations de $f$ pour voir combien de fois la fonction prend la valeur $\frac 1 2$.

Pour cela, commençons par l'étude du signe de $f'(x)$ en fonction de $x$. Comme $\pi >0$, le signe de $f'(x)$ ne dépend que de celui de $-2x+1$ et de $\cos\left( \pi x(1-x) \right)=\cos(w(x))$.

La fonction $w$ est polynomiale du second degré, et on a la factorisation $w(x)=- \pi x(x-1)$.

Elle a deux racines $x_1=0$ et $x_2=1$. Comme le coefficient de $x^2$ est $- \pi <0$ ($w(x)=-\pi x^2+ \pi   x$), $w$ atteint un maximum en $\frac{x_1+x_2}{2}=\frac{0+1}{2}=\frac 1 2$.

On a

• $w\left(\frac 1 2 \right)=\pi \times \frac 1 2 \left(1-\frac 1 2\right)=\frac{\pi}{4}$
• $w\left( 2 \right)=\pi \times 2 \times (1-2)=-2\pi$

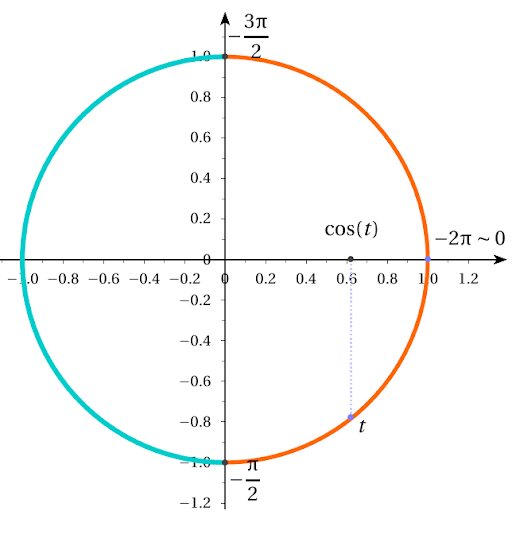
Voici les variations de $w$ et le signe de la fonction $\cos\circ w$ sur $[0,2]$.

Comme la fonction $w$ est continue et strictement décroissante sur $[1;2]$, d'après le théorème des valeurs intermédiaires (TVI), il existe exactement un nombre $\alpha$ et un nombre $\beta$ tels que $1<\alpha<\beta<2$ vérifiant

• $w(\alpha)=-\frac \pi 2$
• $w(\beta)=-\frac{3\pi}{2}$

puisque $0>-\frac \pi 2 > -\frac{3\pi}{2} >-2\pi$.

On peut alors utiliser le signe de la fonction $\cos$ sur $[-2\pi;0]$

Voici ce que l'on peut résumer :

• Lorsque $x$ est compris entre $1$ et $2$, on se sert du tableau ci-dessus pour obtenir le signe de $\cos(w(x))$, avec $t=w(x)$.
• Lorsque $x$ est compris entre $0$ et $1$, on a d'après le premier tableau $0\leq w(x) \leq \frac \pi 4$ donc $\cos(x)>0$.

Cela nous permet de déduire le signe de la fonction $x\longmapsto \cos\left(\frac {\pi^2} 4 x(1-x)\right)$ en fonction de $x$. On a ainsi les variations de la fonctions $f$.

En effet

• $f(0)=\sin(0)=1$
• $f\left(\frac  1 2 \right)=\sin\left(\frac \pi 4 \right)=\frac {\sqrt 2} 2\sim 0.707>0.7$
• $f\left(2 \right)=\sin(-2\pi)=0$

Sur $\left[0;\frac 1 2\right]$, $f$ étant continue et strictement croissante, d'après le TVI, l'équation $f(x)=\frac{\sqrt 2}{2}=0.7$ admet exactement une solution $x_1$.

Puisque $f(1)=0$,  $f$ étant continue et strictement décroissante sur $\left[\frac 1 2 ; 1\right]$, d'après le TVI $f(x)=0.7$ admet exactement une solution $x_2$.

Comme $f$ est strictement décroissante sur $[1;\alpha]$, on a $f(\alpha)<0$.

Concernant les solutions sur l'intervalle $[\alpha;2]$ :

• $f$ étant strictement croissante sur $[\alpha;\beta]$, il ne peut y avoir qu'une seule solution de $f(x)=0.7$ sur $[\alpha;\beta]$.
• $f$ étant strictement décroissante sur $[\beta;2]$, il ne peut y avoir qu'une seule solution de $f(x)=0.7$ sur $[\beta;2]$.

D'après le TVI appliqué à la fonction $f$ continue :

• $f(1,5)\approx 0,71>0,7$ (et $f(1,6)\approx 0.13<0,7$) implique l'existence d'une solution $x_3$ comprise dans l'intervalle $[\alpha;2]$ (plus précisément dans l'intervalle $]1,5;1,6[$).
• $f(1,7)\approx 0,56 <0,7$ (et $f(1,9)\approx 0,79>0,7$) implique l'existence d'une solution $x_4$ comprise dans l'intervalle $]1,7;2[$ (plus précisément dans l'intervalle $]1,7;2[$).

Conclusion.

L'équation $\sin\left( \pi x(1-x) \right)=0,7$ admet exactement $4$ solutions sur l'intervalle $[0;2]$.

Versions téléchargeables

L'énoncé

• version pdf 
• version source tex

La solution

• version pdf
• version source tex

 

D'autres exercices

Un nouvel exercice sur ce blog tous les dimanches.

En attendant, voici la page regroupant tous les exercices du dimanche.