Suites arithmético-géométriques (1) : définitions et exemples

Dans ce billet, nous nous intéresserons à un cas précis de suite récurrentes très représenté dans le programme de maths français, les suites arithmético-géométriques.

On dit qu'une suite réelle $(u_n)$ est récurrente s'il existe une fonction $f:\mathbb R \rightarrow \mathbb R$ tel que pour tout $n\in\mathbb N$, $u_{n+1}=f(u_n)$.

Si $f$ est une fonction affine, c'est-à-dire une fonction du type $f(x)=ax+b$, avec $a$ et $b$ réels, alors on a une suite arithmético-géométrique.  Les suites arithmétiques et et les suites géométriques sont des cas particuliers de suites arithmético-géométriques.

Vocabulaire

Suites arithmétiques

Si $f(x)=x+b$, nous avons une suite arithmétique. Autrement dit, une suite artihmétique est une suite telle que pour tout entier naturel $n\in\mathbb N$, $u_{n+1}=u_n+b$ 

Le réel $b$  est appelé la raison de la suite $(u_n)$.

Exemple 1. La suite des nombres impairs positifs est une suite arithmétique de raison 2, avec $u_0=1$. Nous avons $u_0=1$, $u_1=3$, $u_2=5$, etc.

Propriété 1.

Si $(u_n)$ est une suite arithmétique de raison $b$, alors pour tout $n\in\mathbb N$, 

$u_n=u_0+nb$

Démonstration. On fait une récurrence sur la propriété : $\mathcal P_n$ définie pour tout $n$ par $u_n=u_0+nb$

(1) Initialisation : On a $\mathcal P_0$ car $u_0=u_0+0\times b$

(2) Hérédité : Supposons $\mathcal P_n$ pour un certain $n\in\mathbb N$.

Alors $u_{n+1}=u_n+b =u_0+nb+b=u_0+b(n+1)$ 

On a donc $\mathcal P_{n+1}$.

(3) Conclusion : $\forall n\in\mathbb N, \mathcal P_n$.

La preuve est faite.

Représentation graphique

Suites géométriques

Si $f(x)=ax$, nous avons une suite géométrique. 

Autrement dit, une suite géométrique est une suite telle que pour tout entier naturel $n\in\mathbb N$, $u_{n+1}=au_n$ 

Le réel $a$  est encore appelé la raison de la suite $(u_n)$.

Exemple 2. La suite des puissances de 2 est une suite géométrique de raison 2, avec $u_0=1$. Nous avons $u_0=1$, $u_1=2$, $u_2=2^2$, etc.

Propriété  2.

Si $(u_n)$ est une suite géométrique de raison $a$, alors pour tout $n\in\mathbb N$, 

$u_n=a^nu_0$

Démonstration. On fait une récurrence sur la propriété : $\mathcal P_n$ définie pour tout $n$ par $u_n=a^nu_n$

(1) Initialisation : On a $\mathcal P_0$ car $u_0=a^0u_0$ puisque $a^0=1$.

(2) Hérédité : Supposons $\mathcal P_n$ pour un certain $n\in\mathbb N$.

Alors $u_{n+1}=au_n=aa^nu_0$ 

Alors $u_{n+1}=a^{n+1}u_0$.  

On a donc $\mathcal P_{n+1}$.

(3) Conclusion : $\forall n\in\mathbb N, \mathcal P_n$.

La preuve est faite.

Représentation graphique

Suites arithmético-géométriques

Si $f(x)=ax+b$, nous avons une suite arithmético-géométrique. 

Autrement dit, une suite arithmético-géométrique est une suite telle que pour tout entier naturel $n\in\mathbb N$, $u_{n+1}=au_n+b$ 

Exemple 3. La suite définie par $u_0=0$ et $u_{n+1}=\frac 3 2 u_n+\frac 2 3$ Nous avons $u_0=0$, $u_1=\frac 2 3$, $u_2=\frac 5 3$, etc.

Représentation graphique

• Cas 1 : $|a|>1$ 

• Cas 2 : $|a|<1$
  
  
  
  
  
  
  
  
  
  
  
  
  

Remarque 1. 

1. Si $a=1$, nous avons une suite arithmétique
2. Si $b=0$, nous avons une suite géométrique
3. Si $a=1$ et $b=0$, nous avons une suite constante (on peut montrer que ce sont les seules suites à la fois arithmétiques et géométriques)
4. Si $a=0$, nous avons une suite constante à partir du rang 1. Si de plus, $b=u_0$, alors, nous avons comme dans le cas précédent une suite constante. 
5. Le donnée de $a$ et $b$ suffit à déterminer entièrement une suite arithmético-géométrique ; cependant comme nous le montre les cas (4. et 5.) des suites constantes, pour une suite arithmético-géométrique donnée, il n'y a pas unicité du couple $(a,b)$. (Pour $u_0$ fixé, le couple $(a,b)=(0,u_0)$ donne la même suite que $(a,b)=(1,0)$.) Nous verrons plus tard que dans les autres cas pour une suite arithmético-géométrique, il n'existe qu'un seul couple $(a,b)$ tel que pour tout entier naturel $n$, $u_{n+1}=au_n+b$.

Equations aux différences finies

Une équation linéaire aux différences finies d'ordre $1$ est une équations du type : 

$$s_{n+1}=a(n)s_n+\psi(n)$$

où l'inconnue est une suite $(s_n)$.

Si la fonctions $a$ est une constante, alors l'équation devient 

$$s_{n+1}=as_n+\psi(n)$$

Dans le cas où $\psi$ est une fonction constante, on retrouve comme solutions les suites arithmético-géométriques. 

Les équations linéaires aux différences finies d'ordre $1$ feront l'objet d'un billet futur.

Etude d'un exemple de suite arithmético-géométrique

Intéressons-nous à la suite $(u_n)$ définie par $u_0=3$ et telle que pour tout $n\in\mathbb N$, $u_{n+1}=\frac 1 3 u_n +2$. 

Quelques questions.

• Comment varie cette suite ?
• Cette suite possède-t-elle une limite ? Si cette suite converge, que peut-on dire sur sa vitesse de convergence ?
• Cette suite a-t-elle une expression explicite du type $u_n=f (n)$ ?

Variations de $(u_n)$.

On peut étudier la suite définie pour tout $n\in\mathbb N$ par $d_{n}=u_{n+1}-u_n$.

On conjecture sans problème en ayant calculé quelques valeurs de la suite $(d_n)$ que $(d_n)$ est une suite géométrique de raison $\frac 1 3$. 

On peut par exemple utiliser un script Python comme celui-ci : 

En l'executant, il semble bien de $(d_n)$ est une suite géométrique de raison $\frac 1 3$.

Prouvons-le.  On a pour tout $n\in\mathbb N$

$$d_{n+1}=u_{n+2}-u_{n+1}=\frac1 3 u_{n+1} + 2- \left(\frac1 3 u_{n} + 2\right)$$

$$d_{n+1}=\frac 1 3 u_{n+1} - \frac 1 3 u_{n}=\frac 13 \left(u_{n+1}-{u_{n}} \right)=\frac 1 3 d_{n}$$

La suite $(d_n)$ est donc géométrique, et d'après la propriété 2, pour tout $n\in\mathbb N$, on a $d_{n}=\left(\frac 1 3\right)^n d_0$.

Comme $d_0=u_1-u_0=\frac 1 3 u_0+2-u_0=-\frac 2 3 u_0+2$, on obtient $d_0=-\frac 2 3 \times \frac 1 2+2=\frac 5 3$.

Donc pour tout $n\in\mathbb N$, $d_n=\left(\frac 1 3\right)^n \times \frac 5 3$.

Chaque $d_n$ est positif donc la suite $(u_n)$ est croissante. 

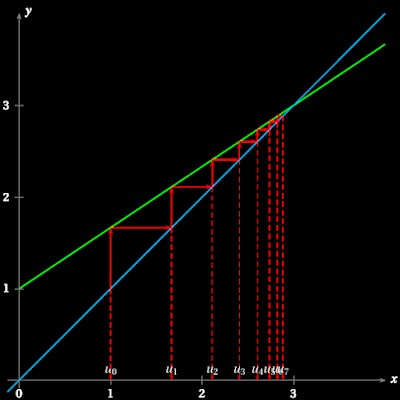
De plus $(u_n)$ semble majorée. En effet, regardons pour cela la représentation graphique de $(u_n)$.

L'abscisse du point d'intersection de la suite de la droite d'équation $y=x$ et de la droite d'équation $y=\frac 1 3 x+2$ semble majorer $(u_n)$. En résolvant l'équation $x=\frac 1 3x +2$, il n'est pas difficile de voir que ce cette abscisse est $3$.

On peut montrer en utilisant le théorème de récurrence que pour tout $n$ entier naturel, $u_n\leq 3$. On en déduit par le théorème de convergence monotone que $(u_n)$ converge. On peut conjecturer graphiquement que la limite de $(u_n)$ est d'ailleurs $3$.  

Remarquons au passage que $u_{n+2}-u_{n+1}=\frac 1 3 (u_{n+1}-u_{n})$, ce qui se traduit par le fait que l'écart entre deux termes consécutifs est multiplié par $\frac 1 3$ à chaque rang.

Recherche d'une forme explicite pour $u_n$.

Notre prochain objectif est de trouver une forme explicite pour la suite $(u_n)$. Ce sera l'objet d'un prochain article de ce blog. Ensuite, nous nous intéresserons au cas général des suites arithmético-géométriques.