Spécialité (Approfondissement) - Exercice 10 (spécial)

Voici un exercice d'approfondissement niveau terminale de la spécialité mathématique.

Des versions téléchargebles (pdf et tex) sont disponibles à la fin de l'article.  

Thèmes. Fonctions exponentielle, continuité, limites, différentiabilité

Niveau Terminale de la spécialité mathématique (approfondissement).

Exercice 10.

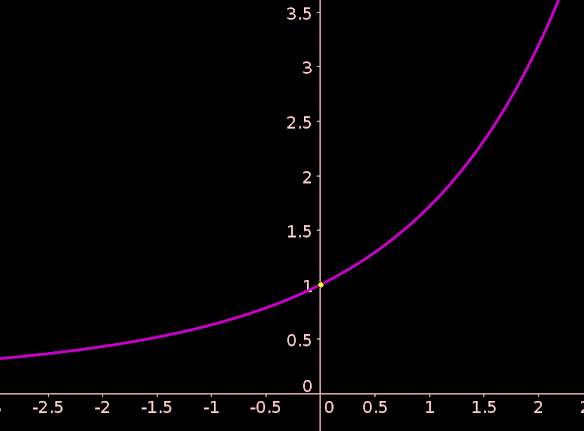
Le but de cet exercice est d'étudier la fonction $x\longmapsto\frac{\mathrm{e}^x -1}{x} $.

On note $f$ la foncion définie sur $\mathbb R$ par

$$\left\{ \begin{array}{rclr} f(x)&=& \frac{\mathrm{e}^x -1}{x} & \textrm{si } x\neq 0 \\ f(0)&=& 1  \end{array} \right. $$

Partie 1 : Continuité et limites

1.  Justifier que $f$ est continue sur $\mathbb R$.
2. Déterminer les limites de $f$ en $-\infty$ et en $+\infty$.

Partie 2 : Inégalités

On  note pour tout $x\in\mathbb R$

•  $u(x)=\mathrm{e}^x-x-1 $
•  $v(x)=\frac{x^2}{2}$
•  $w(x)=\frac{x^2}{2}\mathrm{e}^x$

 

On note aussi pour tout $x\in\mathbb R$

• $a(x)=u(x)-v(x)$
• $b(x)=u(x)-w(x)$

1.     
• (a)    Calculer $a''(x)$.
• (b)    En déduire les variations de $a'$ puis celle de $a$.
• (c)    Déterminer le signe de $a(x)$ en fonction de $x$.
2.  De la même façon, déterminer le signe de $b(x)$ en fonction de $x$ sur l'intervalle $[-4;+\infty[$
3. Justifier que pour tout $x\in[-4;0[$,

    $$(1) \ \ \ \ \ \ \ w(x)<u(x)<v(x)$$
    et que pour tout $x\in]0;+\infty[$,
     $$(2) \ \ \ \ \ \ \ v(x)<u(x)<w(x)$$

Partie 3 : Calcul d'une limite et dérivabilité de $f$

1.  Justifier que $f$ est dérivable sur $]-\infty;0[$ et sur $]0;+\infty[$ et exprimer $f'(x)$ en fonction de $x$ sur ces intervalles.
2. 
   
• Montrer que $\lim_{h\rightarrow 0}\frac{e^h-1-h}{h^2}=\frac  1 2$.
• En déduire que $f$ est dérivable en $0$.
3. Justifier que $f$ est croissante sur $\mathbb R$.
4. La fonction $f'$ est-elle continue sur $\mathbb R $ ?

Versions téléchargeables

• version pdf 
• version source tex

La solution

Etant donnée la longueur exceptionnelle de cet exercice, la solution ici sera accessible une semaine après publication de cet article afin de laisser plus de temps au lecteur.

D'autres exercices

Je publie chaque dimanche un nouvel exercice niveau Première ou Terminale de la spécialité maths.

En attendant, voici la page regroupant tous les exercices du dimanche.