Limite d'une suite

Définition et unicité de la limite d'une suite

Soit $(u_n)$ une suite de nombres réels et $x$ un nombre réel.

On dit que la suite $(u_n)$ converge vers $x$ si : 

$(\ast)$ pour tout $\varepsilon>0$, il existe un entier $N_\varepsilon>0$ tel que pour tout $n>N_\varepsilon$, $x-\varepsilon<u_n<x+\varepsilon$.

On peut reformuler la condition $(\ast)$ avec des quantificateurs  : 

$$(\ast)\ \ \forall \varepsilon>0,\exists N_\epsilon>0, \forall n>N_\varepsilon, x-\varepsilon<u_n<x+\varepsilon$$

Remarque. $N_\varepsilon$ est un entier qui dépend de $\varepsilon$. 

Que veut dire cette définition ? Elle veut dire que pour une précision donnée ($\varepsilon$), il existe un rang ($N_\epsilon$), à partir duquel tous les termes de la suite ne s'éloigneront plus de $\varepsilon$ de $x$.

On dit aux élèves de lycée  : "les termes sont aussi proches que l'on veut de $x$ pourvu que leur rang soit assez grand".

Remarque 1. 

Une suite $(u_n)$ converge vers $x$ si et seulement si la suite $(v_n)$ définie pour tout entier naturel $n$ par $v_n=u_n-x$, converge vers 0. En effet : 

$$x-\varepsilon<u_n<x+\varepsilon \Longleftrightarrow -\varepsilon<u_n-x<\varepsilon$$

Remarque 2.

Dans la définition de la convergence, on peut remplacer l'encadrement $x-\varepsilon<u_n<x+\varepsilon$ par 

$\left|u_n-x\right|<\varepsilon$. 

En effet $\left|u_n-x\right|=\left\{\begin{array}{rcl} u_n-x & \textrm{si} & u_n\geq x \\  x-u_n & \textrm{si} & u_n\leq x  \end{array} \right.$ donc 

$$\left|u_n-x\right|<\varepsilon \Longleftrightarrow \left\{\begin{array}{rcl} u_n-x<\varepsilon & \textrm{si} & u_n\geq x \\  x-u_n<\varepsilon & \textrm{si} & u_n\leq x \end{array} \right.$$

D'où

$$\left|u_n-x\right|<\varepsilon \Longleftrightarrow \left\{\begin{array}{rcl} u_n<x+\varepsilon & \textrm{si} & u_n\geq x \\  x-\varepsilon<u_n & \textrm{si} & u_n\leq x \end{array} \right.$$

Or comme $\varepsilon>0$, si $u_n\geq x$, on a automatiquement $u_n\geq x > x-\varepsilon$ et si $u_n\leq x$, on a automatiquement $u_n\leq x< x+\varepsilon$. On en déduit que 

$$\left|u_n-x\right|<\varepsilon \Longleftrightarrow \left\{\begin{array}{rcl} x-\varepsilon<u_n<x+\varepsilon & \textrm{si} & u_n\geq x \\  x-\varepsilon<u_n<x+\varepsilon & \textrm{si} & u_n\leq x \end{array} \right. \Longleftrightarrow  x-\varepsilon<u_n<x+\varepsilon$$

Propriété. 

Si $(u_n)$ converge vers $x$ et aussi vers $y$, alors $x=y$.

$x$ est alors l'unique nombre vers lequel $(u_n)$ converge et l'on dit que la limite de $(u_n)$ est $x$. 

On note 

$$\lim_{n} u_n=x$$

Démonstration. Faisons une démonstration par l'absurde. On suppose que $x\neq y$.

Sans perte de généralité supposons que $x<y$ et notons $\alpha=\left|x-y\right| >0$.

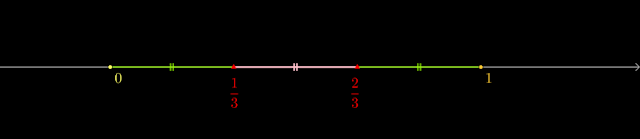
Nous allons faire en sorte de trouver un terme $u_m$ qui soit à la fois suffisamment proche de $x$ et à la fois suffisamment proche de $y$ pour créer une contradiction. Pour cela, on va considérer la distance entre $x$ et $y$ et faire en sorte que $u_m$ soit à moins du tier de cette distance à la fois de $x$ et de $y$ (c'est comme trouver un nombre plus petit que $\frac 1 3$ et plus grand que $\frac 2 3$).

Par définition de convergence vers $x$, il existe un entier $N=N_{\alpha,x}$ dépendant de $\alpha$ et de $x$ tel que 

$$(1)\ \ \ \ \forall n>N, \left| u_n-x\right| <\frac \alpha 3$$

Ici $\varepsilon=\frac \alpha 3$.

Par définition de convergence vers $y$, il existe un entier $N'=N_{\alpha,y}$ dépendant de $\alpha$ et de $y$ tel que 

$$(2)\ \ \ \ \forall n>N', \left| u_n-y\right| <\frac \alpha 3$$

On a donc pour $m=N+N'+1$ ($m$ est plus grand que $N$ et plus grand que $N'$), et d'après (1) et (2) :

$$x-\frac{\alpha}{3}<u_m<x+\frac{\alpha}{3} \ \textrm{et} \ y-\frac{\alpha}{3}<u_m<y+\frac{\alpha}{3}$$

On en déduit en particulier que  

$$(3) \ \ y-\frac \alpha 3<u_m<x+\frac \alpha 3$$  

Mais d'après la construction réalisée (voir dessin), la borne inférieure de l'intervalle autour de $y$ est strictement supérieure et la borne supérieure de l'intervalle autour de $x$. Si on n'en est pas convaincu, il suffit de faire un calcul :

$$y-\frac \alpha 3 = y-\frac{y-x}{3} = \frac{2y+x}{3}$$

$$x+\frac \alpha 3 = x+\frac{y-x}{3}=\frac{2x+y}{3}$$

Or $x<y$ donc $2x<y+x$ puis $2x+y<2y+x$ d'où l'on déduit que $x+\frac \alpha 3$ + $y-\frac \alpha 3$. Il s'en suit que $y-\frac \alpha 3>x+\frac \alpha 3$ contredisant l'inégalité (3).

Par conséquent $x=y$.

Propriété. 

$$\lim_n \frac 1 n = 0$$

Démonstration. Soit $\varepsilon>0$. Nous voulons trouver un entier positif $N=N_\varepsilon$ tel que $n>N$ implique $\left| \frac 1 n \right| < \varepsilon$, c'est-à-dire $\frac 1 n < \varepsilon$. 

Cette dernière inégalité équivaut à $\frac 1  \varepsilon < n$. Soit $N=\lceil \frac 1  \varepsilon \rceil$ la partie entière supérieure de $\frac 1  \varepsilon$ (le plus petit entier strictement supérieur à $\frac 1  \varepsilon$).

Nous avons bien $n>N \Longrightarrow \frac 1 n  < \varepsilon$.

Ceci étant possible pour tout $\varepsilon$, on en déduit que $\lim_n \frac 1 n = 0$.

A suivre

Dans un article futur, nous verrons quelques propriétés concernant les limites.  Elles nous permettrons de déterminer d'autres exemples de limites de suites. 

Avant ça, je publierai un article sur les suites qui ne convergent pas, les suites divergentes.

En attendant, si vous vous intéressez aux suites et à leur convergence, je vous invite à lire l'article Théorème du point fixe en terminale.