Le plan $\mathbb R^2$ (1) : Points, vecteurs et droites

 Le but de cette série d'articles est de revoir la géométrie du plan de niveau collège/lycée en considérant les points comme des couples de rééls. Nous y reverrons les axiomes et les propriétés de la géométrie euclidienne en les démontrant. 

Dans ce premier article, nous définissons le plan comme l'ensemble des couples $(x,y)\in\mathbb R^2=\mathbb R \times \mathbb R$. Ensuite, nous définissons les droites et les vecteurs.

Les points

Le plan est l'ensemble $\mathbb R \times \mathbb R$ et ses éléments sont appelés les points. Les points $M$ sont donc les couples $(x;y)$ avec $x,y$ réels.

On note $M=(x;y)$ ou $M\ (x;y)$ et l'on dit que $x$ et $y$ sont respectivement l'abscisse et l'ordonnée de $M$.

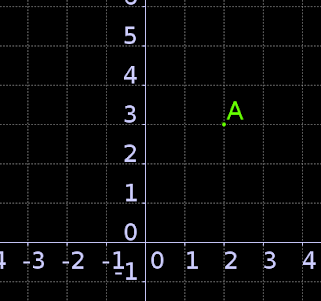
Par exemple, sur la figure ci-dessous, le point on représente le point $A$ de coordonnées $(1;3)$.

 Vecteurs et représentation paramétriques

Un vecteur $\overrightarrow u$ est un couple $\binom{a}{b}$ où $a,b$ sont des nombres réels. 

Les vecteurs sont, comme les points, des éléments de $\mathbb R^2$, mais nous devons nous les représenter de manière différente. On dit que $a,b$ sont les coordonnées de $\overrightarrow u$ et l'on note alors $\overrightarrow u\ \binom a b$.

Par exemple, sont représentés ci-dessous le vecteur $\overrightarrow u$ (deux représentants) de coordonnées $\binom {-1} 3$ et le vecteur  $\overrightarrow w$ de coordonnées $\binom 4 -1$. 

Pour un vecteur $\overrightarrow u$, on note ses coordonnées $\binom{x_{\overrightarrow u}}{y_{\overrightarrow u}}$.

Un vecteur peut être représenté visuellement comme une flèche, c'est-à-dire un objet ayant une direction, un sens et une longueur (nous y reviendrons dans un prochain article). Un vecteur peut être représenté de différentes manières comme on peut le voir sur la figure précédente.

On définit sur $\mathbb R^2$ l'opération $+$ de la manière suivante. Pour tout $\overrightarrow u \ \binom a b$ et $\overrightarrow w \ \binom c d$ : 

$$\overrightarrow u + \overrightarrow w\ \binom{a+c}{b+d}$$

On laisse au lecteur le soin de vérifier que l'addition est associative et commutative. De plus le vecteur nul défini par $\overrightarrow 0\ \binom 0 0$ est l'unique élément neutre de $\mathbb R^2$ en tant qu'espace vectoriel (espace de vecteurs). 

On définit sur l'espace des vecteurs $\mathbb R^2$ la multiplication par les scalaires, c'est-à-dire la multiplication par un élément externe réel. Soit $k\in\mathbb R$ et $\overrightarrow u \ \binom a b$, on note $$k \overrightarrow u \ \binom {ka} {kb}$$

La multiplication par les scalaires se "comporte bien" avec l'addition dans le sens où elle est distributive par rapport à l'addition. Cela se traduit par les deux faits suivants :

Pour tous $k\in\mathbb R$, $\overrightarrow u,\overrightarrow v\in\mathbb R^2$ : $$k(\overrightarrow u + \overrightarrow v)=k\overrightarrow u + k\overrightarrow v$$

Pour tous $k,t\in \mathbb R$, $\overrightarrow u\in \mathbb R^2$ : $$(k+t)\overrightarrow u=k\overrightarrow u + t\overrightarrow u$$

Ainsi muni de $+$ et de la multiplication par les scalaires, on dit que  $\mathbb R^2$ est un espace vectoriel.

Si $A \left(x_A;y_A\right),B \left(x_B;y_B\right)$ sont deux points, alors on définit le vecteur $\overrightarrow{AB}\ \binom{x_B-x_A}{y_B-y_A}$. On le représente comme ci-dessous.

Remarque. $\overrightarrow{AB}=-\overrightarrow{BA}$.

Propriété 0 (Relation de Chasles). 

Si $A,B,C$ sont trois points, on a $\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{BC}$.

Preuve. 

En effet $x_C-x_A=x_C-x_B+x_B-x_A$ et $y_C-y_A=y_C-y_B+y_B-y_A$. 

Vecteurs colinéaires

On dit que deux vecteurs $\overrightarrow u$ et $\overrightarrow v$ sont colinéaires s'il existe un réel non nul $k$ tel que $\overrightarrow u = k \overrightarrow v$.

On peut vérifier que pour les vecteurs la colinéarité est une relation d'équivalence. En particulier, c'est une relation symétrique car si $\overrightarrow u = k \overrightarrow v$, on a  $\overrightarrow v = \frac 1 k \overrightarrow u$

Droite dirigée par un vecteur

Soit $A \ \left(x_A;y_A\right)$ un point du plan et $\overrightarrow u\ \binom a b$ un vecteur non nul (ie tel que $a$ et $b$ ne soient pas tous deux nuls). Alors l'ensemble des points $M\ (x;y)$ tels que $M=A$ ou tels que $\overrightarrow{AM}$ est colinéaire à $\overrightarrow u$ est appelée une droite. 

On dit que c'est la droite passant par $A$ et dirigée par $\overrightarrow u$. $\overrightarrow u$ est alors appelé vecteur directeur de cette droite.

La droite passant par $A$ et dirigée par $\overrightarrow u$ est donc composée des points $M\ (x;y)$ tels qu'il existe $k\in \mathbb R$, tels que $\overrightarrow{AM}=k\overrightarrow u$, puisque le cas $A=M$ correspond au cas où $k=0$.

On note $\mathcal D(A,\overrightarrow u)$ le droite passant par $A$ et dirigée par $\overrightarrow u$.

Remarques. 

(1) Si  $B\in \mathcal D(A,\overrightarrow u)$, alors $\mathcal D(A,\overrightarrow u)=\mathcal D(B,\overrightarrow u)$

(2) Si $\overrightarrow v=\alpha \overrightarrow u$ avec $\alpha\in \mathbb R$, $\alpha\neq 0$ alors, $\mathcal D(A,\overrightarrow u)=\mathcal D(A,\overrightarrow v)$.

Preuves.

(1) On a $\overrightarrow{AB}=t \overrightarrow{u}$ pour un certain $t\in\mathbb R$. Si $t=0$, $A=B$ donc $\mathcal D(A,\overrightarrow u)=\mathcal D(B,\overrightarrow u)$. 

Supposons $t\neq 0$. Si $M\in \mathcal D(A,\overrightarrow u)$, alors il existe $k\in \mathbb R$ tel que 

$\overrightarrow{AM}=k\overrightarrow{u}$. Donc d'après la relation de Chasles, $\overrightarrow{BM}=\overrightarrow{BA}+\overrightarrow{AM}=-t\overrightarrow u+k\overrightarrow u=(k-t)\overrightarrow u$, ainsi $M\in  \mathcal D(B,\overrightarrow u)$. 

On a donc l'inclusion $\mathcal D(A,\overrightarrow u) \subset \mathcal D(B,\overrightarrow u)$. 

De la même façon, comme $\overrightarrow{BA}=-t \overrightarrow{u}$, on montre que si $M\in D(B,\overrightarrow u)$, alors $M\in D(A,\overrightarrow u)$. 

D'où $\mathcal D(B,\overrightarrow u) \subset \mathcal D(A,\overrightarrow u)$.

Pour finir,  $\mathcal D(B,\overrightarrow u) = \mathcal D(A,\overrightarrow u)$

(2) En effet si $\overrightarrow{AM}=k\overrightarrow v$ et que $v=\alpha \overrightarrow u$, alors $\overrightarrow{AM}=k\alpha \overrightarrow u$. Donc $\mathcal D(A,\overrightarrow v)\subset \mathcal D(A,\overrightarrow u)$. Comme $\overrightarrow u = \frac 1 \alpha \overrightarrow v$, on obtient de même que $\mathcal D(A,\overrightarrow u)\subset \mathcal D(A,\overrightarrow v)$.

On a donc la double inclusion. 

 

Ainsi $M(x;y)\in \mathcal D(A,\overrightarrow u) \Longleftrightarrow \left\{\begin{array}{ccc} x-x_A & =&k x_{\overrightarrow u}\\ y-y_A & =& k  y_{\overrightarrow u}  \end{array}\right.$ avec $k\in\mathbb R$. 

Et donc 

$$M(x;y)\in \mathcal D(A,\overrightarrow u) \Longleftrightarrow\exists k\in\mathbb R, \ \left\{\begin{array}{ccc} x & =&x_A+k x_{\overrightarrow u}\\ y & =&y_A+ k  y_{\overrightarrow u}  \end{array}\right.$$

C'est une représentation paramétrique de paramètre $k$ de la droite $\mathcal D(A,\overrightarrow u)$.

Propriété 1. 

Si $A,B$ sont deux points distincts, alors il existe une unique droite passant par $A$ et $B$. On note cette droite $(AB)$.

Démonstration. 

On considère la droite $\mathcal D$ passant par $A$ et dirigée par $\overrightarrow{AB}$. Clairement $B\in\mathcal D$ car $\overrightarrow {AB}= 1 \overrightarrow{AB}$. 

Supposons que $\mathcal D'$ est une droite passant par $A$ et par $B$. Montrons que $\mathcal D'$ est $\mathcal D$. Comme $A\in\mathcal{D'}$, d'après la remarque (1) précédente, on peut supposer que  tel que $\mathcal D'=\mathcal D(A,\overrightarrow u)$ pour un certain vecteur $\overrightarrow u$. Comme $B\in\mathcal D'$, $\overrightarrow{AB}=k\overrightarrow u$ pour un certain $k\in \mathbb R$. Comme $A\neq B$, $k\neq 0$, et d'après la remarque 2 précédente, $\mathcal D'=\mathcal D(A;\overrightarrow{AB})=\mathcal D$.

Propriété 2. 

Pour toute droite $\mathcal D$, il existe des réels $a,b,c$ avec $a,b$ non tous deux nuls tels que $ax+by+c=0$. Plus précisément, si $\overrightarrow u$ dirige $\mathcal D$, on peut prendre $a=-x_{\overrightarrow u}$ et $b=y_{\overrightarrow u}$.

Démonstration. 

Notons $a=-y_{\overrightarrow u}$ et $b=x_{\overrightarrow u}$. Soit $A\in \mathcal D$. Choisissons $c$ de sorte que $ax_A+by_A+c=0$, c'est-à-dire tel que $c=y_{\overrightarrow u}x_A-x_{\overrightarrow u}y_A$.

Soit $M\ (x;y)$ un point de $\mathcal{D}$. Alors il existe $k\in \mathbb R$ tel que $$\left\{\begin{array}{ccc} x & =&x_A+k x_{\overrightarrow u}\\ y & =&y_A+ k  y_{\overrightarrow u}  \end{array}\right.$$

On a 

$$ax+by+c=-y_{\overrightarrow u}\left(x_A+k x_{\overrightarrow u} \right)+x_{\overrightarrow u}\left(y_A+ k  y_{\overrightarrow u} \right)+y_{\overrightarrow u}x_A-x_{\overrightarrow u}y_A=0$$

Donc tous les points de $\mathcal D$ vérifient $ax+by+c=0$.

Propriété 3. 

Tout ensemble de points $M$ dont les coordonnées $(x;y)$ vérifient une équation de la forme $ax+by+c=0$ pour des réels $a,b,c$ avec $a,b$ non tous deux nuls, est une droite.

Démonstration. 

Plusieurs cas sont à étudier.

Si $a=0$, alors la relation est $by+c$ avec $b\neq 0$. Cette relation est donc équivalente à 

$$(0) \ \ \ \ y=-\frac c b$$

Prenons $A\ \left(0;-\frac c b \right)$ et $B\ \left(1;-\frac{c}{b} \right)$. Ce sont deux points dont les coordonnées vérifient l'équation. Notons $\mathcal D$ La droite de vecteur directeur $\overrightarrow {AB}$ de coordonnées $\binom 1 0$, et montrons que l'ensemble des points $M\ (x;y)$ vérifiant $(0)$ est la droite $\mathcal D$. 

Si $M$ vérifie $(0)$, alors $M\ \left(x;-\frac c b\right)$, et $\overrightarrow{AM}$ a pour coordonnées $\binom x 0$ donc $\overrightarrow{AM}=x\overrightarrow u$ ce qui prouve que $M\in \mathcal D$. 

Réciproquement, si $M\ (x;y)\mathcal D$, alors $\overrightarrow{AM}=k\overrightarrow u$ pour un certain réel $k$. Comme $\overrightarrow{AM}$ a pour coordonnées $\binom{x}{y+\frac c b}$ et que $k\overrightarrow u$ a pour coordonnées $\binom{k}{0}$, on en déduit que $k=x$ et que $y=-\frac{c}{b}$. Ainsi $(x;y)$ vérifie $(0)$.

De la même façon, si $b=0$, les coordonnées $(x;y)$ du point $M$ vérifient 

$ax+by+c=0$ si et seulement s'ils vérifient

$$(0') \ \ \ \ x=-\frac c a$$

De manière similaire au cas où $a=0$, on montre que $(x;y)$ vérifient $(0')$ si et seulement si ce sont les points de la droite $\mathcal D$ passant par les points $A\ \left(-\frac c a;0 \right)$ et $B\ \left( -\frac c a;1\right)$. 

Supposons maintenant que $a\neq 0$ et que $b\neq 0$. $M\ (x;y)$ est tel que $ax+by+c=0$ si et seulement si $\frac{a}{b}x+y+\frac{c}{b}=0$ c'est-à-dire si et seulement si 

$$(1)\ \ \ \ y=-\frac{a}{b}x-\frac{c}{b}$$

Notons $A$ et $B$ les points de coordonnées respectives $\left(0;-\frac c b \right)$ et $\left(1;-\frac {a+c} b \right)$. Ce sont des points dont les coordonnées vérifient $(1)$. 

Nous allons montrer que la droite $(AB)$ est l'ensemble des points dont les coordonnées $(x;y)$ vérifient $(1)$.

Si $M\in(AB)$ a pour coordonnées $(x;y)$, alors il existe $k\in \mathbb R$ tel que $\overrightarrow{AM}=k\overrightarrow{AB}$. Ainsi en identifiant les coordonnées des vecteurs, on a $x=k$ et $y+\frac c b=-\frac a b$. Cette dernière égalité impliquant $(1)$. 

Réciproquement si le coordonnées $(x;y)$ de $M$ vérifient $(1)$, alors $M\ \left(x;-\frac{a}{b}x-\frac{c}{b}\right)$, d'où $\overrightarrow{AM}\ \binom{x}{-\frac{a}{b}x}$  et $\overrightarrow{AB}\ \binom{1}{-\frac a b}$  d'où $\overrightarrow{AM}=x\overrightarrow{AB}$. Donc $M\in (AB)$.

Définition. Pour une droite $\mathcal D$ caractérisée une relation de la forme, 

$$ax+by+c=0$$

On dit que cette relation est une équation cartésienne de $\mathcal D$.

Dans la preuve de la propriété précédente, on a vu que : 

• Si $a=0$, la droite d'équation cartésienne $ax+by+c=0$ a pour vecteur directeur $\overrightarrow u\ \binom{1}{0}$.
• Si $b=0$, la droite d'équation cartésienne $ax+by+c=0$ a pour vecteur directeur $\overrightarrow u\ \binom{0}{1}$. 
• Si $a\neq 0$ et $b\neq 0$, la droite d'équation cartésienne $ax+by+c=0$ a pour vecteur directeur $\overrightarrow u\ \binom{1}{-\frac a b}$.

Dans tous les cas le vecteur $\overrightarrow v\ \binom{-b}{a}$ est un vecteur non-nul colinéaire à $\overrightarrow u$. C'est donc un vecteur directeur de la droite. 

Nous avons donc la propriété très utile suivante 

Propriété 4. 

La droite d'équation cartésienne 

$$ax+by+c=0$$

admet pour vecteur directeur le vecteur de coordonnées $\binom{-b}{a}$. 

Ensuite

Dans le prochain article de cette série, nous définirons le parallélisme et l'orthogonalité des droites. Pour cette dernière définition nous aurons besoin d'introduire le produit scalaire.