La fonction racine carrée

 Dans cet article, nous supposons connus :

• la continuité des fonction réelles (de niveau terminale)
• le théorème des valeurs intermédiaires (de niveau terminale)
• le sens de variations des fonctions (niveau seconde)
• la notion de nombre dérivé et de fonction dérivée (niveau première)
• la fonction carrée $x\mapsto x^2$ (niveau seconde)

Un exemple d'utilisation du théorème des valeurs intermédaires est la justification de l'existence de la fonction racine carrée. Après avoir défini la fonction racine carrée, nous voyons quelques une de ses propriétés :

• Sa croissance
• sa continuité
• sa dérivabilité (sauf en zéro)

La racine carré d'un nombre

Soit $y$ un nombre positif ou nul, on cherche un nombre $x\geq 0$ tel que $x^2=y$.

Pour prouver l'existence d'un tel nombre, nous avons besoin de la continuité  de la fonction carrée. Le théorème des valeurs intermédiaires permettra alors de conclure.

Propriété. 

Pour tout $b\geq 0$, il existe un unique nombre $a\geq 0$ tel que $a^2=b$.

Démonstration. 

Soit $b\in ]0;+\infty[$.

La fonction $f$ définie sur $[0;+\infty[$ par $f(x)=x^2$ est polynomiale donc dérivable (et continue). La dérivée de $f$, $f'$ est telle que $f'(x)=2x$ pour tout $x\geq 0$. Pour $x> 0$, $2x> 0$, donc $f$ est strictement croissante sur $]0;+\infty[$.

On a $f(0)=0$ et $\lim_{x\longrightarrow +\infty} f(x)=+\infty$. 

$f$ étant continue et $b\in ]0;+\infty[ $, on déduit du théorème des valeurs intermédiaires qu'il existe un unique $a\in ]0;+\infty[$ tel que $f(a)=b$.

Comme $x^2=0 \Longleftrightarrow x=0$ (d'après la règle produit nul), le seul nombre $a$ tel que $f(a)=0$ est $0$.

Définition. 

Pour tout $x\geq 0$, on note $\sqrt x$ le seul nombre positif ou nul tel que ${\sqrt x}^2=x$.

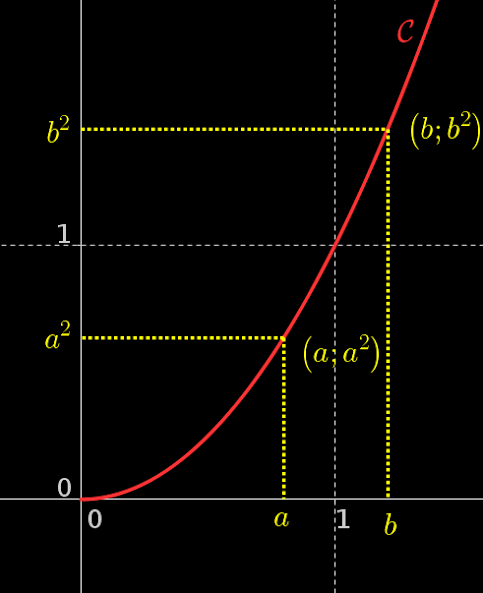
Ci-dessous la fonction carrée représentée par $\mathcal C$ et la fonction racine carrée représentée par $\mathcal R$.

Racine carrée et valeur absolue

Pour la définition de la valeur absolue $\left| x \right|$ d'n nombre $x$, on pourra consulter Valeur absolue d'un nombre réel. 

Propriété 1. 

Si $a$ est un nombre réel, alors $\sqrt{a^2}=\left|a\right|$.

Preuve. 

$\left|a\right|$ est égal à $a$ ou $-a$ donc $\left|a\right|^2=a^2$.

$=\left|a\right|$ est donc l'unique nombre positif ou nul dont le carré est $a^2$.

Propriété 2.

1. Si $a>0$ et $b>0$, alors $\sqrt{ab}=\sqrt{a}\sqrt{b}$.
2. Si $a$ et $b$ sont deux réels de même signe, alors $\sqrt{ab}=\sqrt{\left|a\right|}\sqrt{\left|b\right|}$

Preuve. 

1. $\sqrt{a}$ et $\sqrt{b}$ sont positif ou nul et leur produit $\sqrt{a}\sqrt{b}$ l'est aussi. Le carré de $\sqrt{a}\sqrt{b}$ vaut $ab$ donc $\sqrt{a}\sqrt{b}$ est la racine carrée de $ab$.
2. Si $a$ et $b$ sont positifs ou nuls, on est dans le cas (1).
   
   Supposons $a$ et $b$ négatifs ou nuls. Alors $ab=(-a)(-b)$, avec $-a\geq 0$ et $-b\geq 0$ donc d'après le cas (1), $\sqrt{ab}=\sqrt{(-a)(-b)}=\sqrt{-a}\sqrt{-b}=\sqrt{\left|a\right|}\sqrt{\left|b\right|}$.

Croissance de la fonction $\sqrt {\cdot }$ 

La fonction carrée est strictement croissante sur $[0;+\infty[$. 

Ainsi $0\leq a<b$ implique $a^2< b^2$. 

Soit $x$ et $y$ tels que $0\leq x<y$, si $\sqrt x \geq \sqrt y$, alors $x=y$ et $x^2=y^2$, ou bien d'après la remarque précédente, $x> y$ contredisant $x<y$. 

$0\leq x<y$ implique donc $\sqrt x < \sqrt y$ d'où l'on peut déduire que fonction racine carrée est strictement croissante. 

En particulier $0\leq x\leq y$ implique $\sqrt x \leq  \sqrt y$.

On notera $\sqrt \cdot$ la fonction $[0;+\infty[\longrightarrow [0;+\infty[$, qui à un nombre $x$ associe le nombre $\sqrt x$.

Continuité de la fonction $\sqrt {\cdot }$ 

Pour montrer que $\sqrt{\cdot } $ est continue, il suffit de montrer que pour tout $x$, $\lim_{t\longrightarrow x}\sqrt{t}=\sqrt x$.

Soit $x\geq 0$ et $t\geq 0$, avec $t\neq x$. 

On pose $h=t-x$, d'où $t=x+h$, avec $h\neq 0$.

Pour $-\frac x 2<h<\frac x 2$, on a $0 \leq \frac x 2<x+h<3\frac x 2 $.

Ainsi on a 

$$\sqrt{x+h}-\sqrt{x}=\frac{\left(\sqrt{x+h}-\sqrt{x}\right)\left(\sqrt{x+h}+\sqrt{x}\right)}{\sqrt{x+h}+\sqrt{x}}=\frac{\sqrt{x+h}^2-\sqrt{x}^2}{\sqrt{x+h}+\sqrt{x}}$$

D'où

$$\sqrt{x+h}-\sqrt{x}=\frac{x+h-h}{\left(\sqrt{x+h}+\sqrt{x}\right)}=\frac{h}{\left(\sqrt{x+h}+\sqrt{x}\right)}$$

Donc comme $\sqrt{x+h}\geq \sqrt{\frac x 2} $ par croissance de $\sqrt {\cdot }$, on en déduit que $\sqrt{x+h}+\sqrt{x}\geq \sqrt{\frac x 2}+\sqrt{x}=\left(\sqrt{\frac 1 2} + 1\right)\sqrt x $ puis que 

$$\sqrt{x+h}-\sqrt{x}\leq \frac{h}{\left(\sqrt{x+h}+\sqrt{x}\right)}\leq \frac{h} {\left( \sqrt{\frac 1 2} + 1\right) \sqrt x}$$

Soit $\varepsilon>0$. On a 

$${\left(\sqrt{x+h}+\sqrt{x}\right)}\leq \frac{h} {\left( \sqrt{\frac 1 2} + 1\right) \sqrt x} \leq \varepsilon \Longleftrightarrow h \leq \varepsilon {\left( \sqrt{\frac 1 2} + 1\right) \sqrt x}$$

Posons $\alpha=\alpha_x=\min\left(\frac x 2, \varepsilon {\left( \sqrt{\frac 1 2} + 1\right) \sqrt x} \right) $. Alors pour tout $h$ tel que $-\alpha_x<h<\alpha_x$, on a donc $\sqrt{x+h}-\sqrt{x}\leq \varepsilon$. 

On en déduit que $\lim_{h\longrightarrow 0}\sqrt{x+h}=\sqrt x $, ou encore que $\lim_{t\longrightarrow x}\sqrt{t}=\sqrt x$ d'où l'on conclue à la continuité de $\sqrt \cdot$ en $x$. 

Ceci étant vrai pour tout $x\geq 0$, $\sqrt \cdot$ est donc continue.

Limite de $\sqrt \cdot$ en $+\infty$

Soit $A>0$, alors pour tout $x\geq A^2$, on a $\sqrt{x}\sqrt{A^2}=A$.

Ceci prouve que $\lim_{x\longrightarrow +\infty} \sqrt x=+\infty$.

 

\subsection{Dérivabilité de la fonction $\sqrt \cdot$}

Notons $r$ la fonction $[0;+\infty[ \longrightarrow [0;+\infty[$, tel que $r(x)=\sqrt x$

On veut estimer pour tout $x\geq 0$ la limite 

$$\lim_{h\longrightarrow 0}\frac{\sqrt{x+h}-\sqrt{x}}{h} $$

Cas où $x\neq 0$.

On a comme précédemment,

$$ \frac{\sqrt{x+h}-\sqrt{x}}{h}=\frac{\frac{h}{\sqrt{x+h}+\sqrt{x}}}{h}=\frac 1 {\sqrt{x+h}+\sqrt{x}}$$

Puisque la fonction $r=\sqrt{\cdot }$ est continue, $\lim_{h\longrightarrow 0}\sqrt{x+h}=\sqrt x$. Alors 

$$\lim_{h\longrightarrow 0}\frac{\sqrt{x+h}-\sqrt{x}}{h}=\lim_{h\longrightarrow 0}\frac 1 {\sqrt{x+h}+\sqrt{x}}=\frac {1}{2\sqrt x}$$

On en déduit que lorsque $x\neq 0$, le nombre dérivé $r'(x)$ existe et vaut $\frac 1 {2\sqrt x}$.

Si maintenant $x=0$, on a pour $h\neq0$, $h>0$,

$$\frac{\sqrt{x+h}-\sqrt{x}}{h} =\frac{\sqrt{h}}{h}=\frac{\sqrt h}{\sqrt h \sqrt h}=\frac{1}{\sqrt h} $$

Soit $A>0 $. Comme $\lim_{x\longrightarrow +\infty} \sqrt x=+\infty$, il existe $\alpha>0$ tel que si $x\sqrt \alpha$, $\sqrt x> A$. 

Alors pour tout $h>0 $ tel que  $0<h<\frac 1 A$, on a $\frac 1 h > A$ et $\frac 1 {\sqrt{h}}=\frac{\sqrt 1}{\sqrt{h}}= \sqrt{\frac 1 h}>A$.

Ainsi $\lim_{h\longrightarrow 0}\frac{1}{\sqrt h}=+\infty$, d'où $r$ n'est pas dérivable en $0$.

Et ensuite

Toute fonction continue $f$ strictement monotone sur un intervalle de $\mathbb R$ admet une fonction réciproque $f^{-1}$, c'est-à-dire une fonction vérifiant $f^{-1}\circ f (x)=x$ et $f\circ f^{-1}(y)=y$. 

C'est un sujet que j'aimerai aborder par la suite. Nous pourrons y voir la fonction $\ln$ comme réciproque de la fonction exponentielle, les fonction $\arccos$ et $\arcsin$ comme fonction réciproques respectives des fonctions $\cos$ et $\sin$ sur des intervalles bien choisis...